Fractal-dimension method (FDM).
Метод фрактальной размерности для прослеживания первых вступлений.
Фрактал по определению - это множество в метрическом пространстве, для которого размерность Хаусдорфа-Безиковича сильно превышает топологическую размерность (Мандельброт, 1983).
Размерность Хаусдорфа-Безиковича обобщает топологическое понятие заданной размерности для неотрицательных действительных значений. В случае кривой на плоскости, кривая имеет фрактальную размерность D, который находится в диапазоне 1 <= D <= 2. Можно сказать, что фрактальная размерность количественно отражает степень сложности фрактальной кривой. Теоретическую основу фрактальной теории можно найти у Мандельброта (1983), Федера (1988), и др. Использование фракталов в геофизике полностью описано Теркоттом(1997) и Корвином (1992). Фрактальные кривые могут быть классифицированы как самоподобные или самоаффинные. Фрактальная размерность самоафинного фрактала определяется как
![]()
Для временных рядов, эквивалентное определение самоаффинного фрактала требует, чтобы вариограмма V(h) вела себя как (Теркотт, 1997)
![]()
где V(h) определяется как математическое ожидание квадратов разностей выборок временных рядов s(t), разделенных задержками h. В соответствии с другими авторами (например, Тоси др., 1999; Цзяо и Луна, 2000), сейсмические трассы удовлетворяют этому требованию и могут быть классифицированы как самоаффинные фракталы.
"Метод вариограмм" Корвина (1992), является одним из наиболее подходящих и надежных методов расчета фрактальной размерности самоаффинных кривых. Уравнения (6) и (7) можно переписать как:
![]()
На практике V(h) вычисляется для различных задержек h и затем рисуется в билогарифмическом масштабе как рисунок Мандельброта-Ричардсона. Фрактальная размерность D определяется наклоном b
прямой линии на рисунке Мандельброта-Ричардсона
![]()
В статье
Juan I. Sabbione and Danilo Velis. Automatic first-breaks picking: New strategies and algorithms. GEOPHYSICS,VOL. 75, NO. 4, 2010; P. V67–V76
представлен разработанный авторами статьи метод фрактальной размерности (FDM) для обнаружения первого вступления, основанный на том, что случайный шум имеет более высокую фрактальную размерность, чем, чем сигнал. Фрактальная размерность белого шума равна 2, в то время как фрактальная размерность коррелированного теоретической сигнала равна 1. Таким образом, начало первого вступления может быть определено путем обнаружения фрактальной размерности перехода от шума к сумме шума и сигнала.
В методе FDM фрактальная размерность оценивается в скользящем окне длиной nf и ее значение присваивается последней выборке окна. Опыт показывает, что если nf слишком мало, вариограмма и фрактальная размерность не могут быть оценены адекватно. С другой стороны, если nf слишком большое, то быстрые изменения фрактальной размерности не будут определено правильно. Цзяо и Луна (2000) анализировали различные длины окна и рекомендуют использовать окно 48 образцов. Учитывая эту информацию, и принимая во внимание период сигнала T, авторы статьи рекомендуют устанавливать
размер окна nf=k*T, где k - целое число k>=48*(T/2). (T задано в отсчетах).
В случае присутствия перед первыми вступлениями коррелированого шума (как в методе вибросейс) существенное улучшение метода FDM получается, если в сейсмическую трассу добавить фоновый шум. Этот эффект может быть объяснен тем, что добавка фонового шума, уничтожает структуру коррелированного шума. до первого вступления.
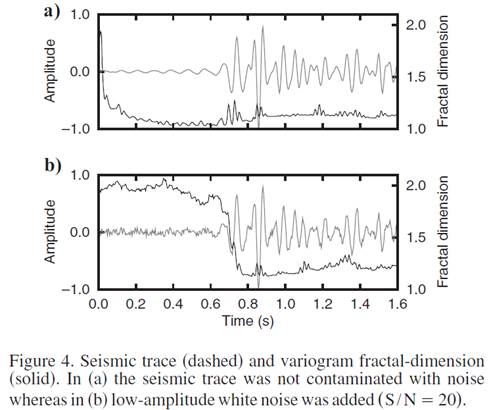
Рекомендуется добавлять всегда низкоамплитудный белый шум к данным при использовании FDM.
Количество добавляемого шума тестируется на конкретных данных, поскольку зависит от фонового шума сейсморазведки. Эта простая стратегия значительно улучшает возможности FDM для прослеживания первых вступлений.
FDM можно резюмировать следующим образом: Рассмотрим скользящее окно в сейсмотрассе s(t) (с добавленным шумом) и оценим его вариограмму V(h,T) используя
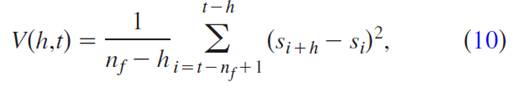
для четырех задержек h=1, 2, 3 и 4, адекватных захватить шероховатости в шумной сейсмотрассе. После установки прямой линии на билогарифмическом рисунке Мандельброта-Ричардсона, мы оцениваем
фрактальную размерность D с использованием уравнения (9) и присваиваем ее значение последней выборке окна. Впоследствии можно использовать EPS фильтр для повышения качества определения первого вступления. Рекомендуется устанавливать длину фильтра EPS равной 1.5 периода. Наконец, поскольку фрактальная размерность уменьшается с приходом сигнала, мы определяем точку первого вступления по выборке с минимальным значением производной EPS.
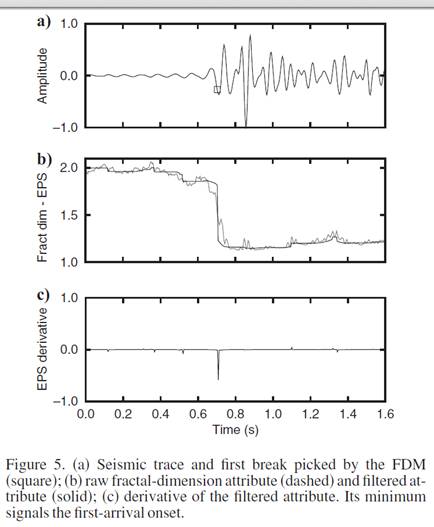
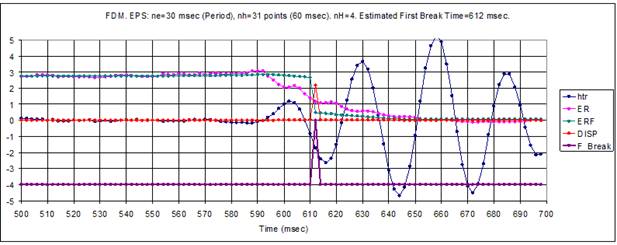
В этом случае добавлен белый шум из расчета S/N=20, где S/N вычисляется как отношение энергии трассы к энергии шума. Поскольку период первого вступления равен примерно 20 отсчетов, тут установлены nf=60 и ne=30.
Ниже представлен пример из программы HEADW.