Опции проекта Depth Imaging.
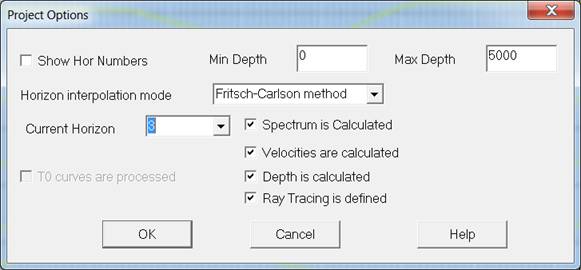
Current Horizon – изменить номер текущего горизонта.
Можно уменьшить этот номер для повторного расчета скоростей и глубин.
T0 curves are processed – Если снять этот флажок, то будут загружаться
первоначальные линии T0 из файла горизонтов, в противном случае – из файла обработанных линий T0.
Velocities are calculated – Если снять этот флажок,
то становится возможным обрабатывать по текущему горизонту начальные скорости и производные T0.
Depth is calculated – Если снять этот флажок,
то становится возможным по текущему горизонту заново рассчитать глубины, углы и пластовые скорости.
Ray Tracing is defined – Если снять этот флажок, то
по текущему горизонту отменяется трассирование лучей.
Show Hor Numbers – При включенном флажке подписываются номера горизонтов.
Min Depth – Минимальное значение глубины при отрисовке глубинных разрезов.
Ось глубин направлена вниз. При отработке от рельефа следует указывать отрицательное число.
Max Depth – Максимальное значение глубины при отрисовке глубинных разрезов.
Ось глубин направлена вниз.
Horizon interpolation mode – способ пересчета точек X(pk) и Z(pk) в глубины Z(pk).
Это необходимо перед построением модели для трассирования лучей.
Пользователю предоставляется на выбор 4 способа сплайн-интерполяции:
-
Akima's method (continuous 1st derivatives, only);
-
Fritsch-Carlson
method (continuous 1st derivatives, only);
-
Cubic spline (continuous 1st and 2nd derivatives)
-
Hermite Polynomial (continuous 1st derivatives, only).
Лучше всего подходит интерполяция “Fritsch-Carlson method”. Это такой вариант сплайнов, который наилучшим образом сохраняет монотонность функции.
Тексты процедур интерполяции взяты из пакета SU Colorado School of Mines
http://www.cwp.mines.edu/cwpcodes
voice mail:
(303) 273-3049; facsimile: (303) 273-3478.
Other References:
Akima, H., 1970, A new
method for interpolation and smooth curve fitting based on local procedures,
Journal of the ACM, v. 17, n. 4, p. 589-602.
Fritsch, F. N., and Carlson,
R. E., 1980, Monotone piecewise cubic interpolation: SIAM J. Numer. Anal., v. 17, n. 2, p. 238-246.
Kahaner, D., Moler, C., and Nash, S., 1989, Numerical Methods and
Software, Prentice Hall.
Greville,
T.N.E, 1969, Theory and Applications of Spline
Functions, Academic Press.