Программа NIP_TOMO.

Чрезвычайно острой в сейсморазведке остается проблема пересчета скоростей ОГТ в интервальные скорости. Еще более актуальной является задача получения сетки мгновенных скоростей, необходимой для глубинной миграции.

Ериком Дувеником разработан и реализован алгоритм томографического расчета сетки скоростей V(x,z) и V(x,y,z) по параметрам CRS.

Литература: “Tomographic determination of seismic velocity models with kinematic wavefield attributes”,

DISSERTATION von Dipl.-Geophys. Eric Duveneck, Bremen.

eric.duveneck@gpi.uni-karlsruhe.de

Н.Голярчуком предложен алгоритм пересчета результатов погоризонтного анализа Vогт в параметры CRS.

Этот алгоритм реализован в пункте меню программы CDPS Processing->HORSP-TOMO.

В диалоговом окне Tomography следует указать параметры:

Path for Files - Путь, где размещены все входные и выходные файлы.

Dimension - Размерность задачи:

                            1-D inversion - Одномерная обратная задача.

                            2-D inversion  - Двумерная обратная задача.

                            3-D inversion  - Трехмерная обратная задача.

                            1-D modelling - Одномерная прямая задача.

                            2-D modelling - Двумерная прямая задача.

                            3-D modelling - Трехмерная прямая задача.

В группе "File Names":

Input data file name - Главный входной файл для программы.

При инверсии является выходным файлом процедуры CDPS Processing->HORSP-TOMO. Содержит четыре параметра: Т, M_h, p_xi и xi.

При моделировании содержит скоростную модель среды (интервальные скорости).

Обязательный параметр.

Output Data File Name - Выходной файл параметров CRS в текстовом формате.

Knot sequence in x-direction - Файл узловых точек по оси Х.

Knot sequence in y-direction - Файл узловых точек по оси Y.

Knot sequence in z-direction - Файл узловых точек по оси Z.

Input Velocities - Файл, содержащий априорную информацию о скоростях.

Output Velocities - Уточненный файл априорной информации в результате решения.

Initial velocity model - Начальная скоростная модель.

Final velocity model - Окончательная скоростная модель в формате сейсмического файла SU.

Преобразование файла в формат SPS-PC осуществляется утилитой Seismic Unix.

Epsilon XX Model - Веса для регуляризации решения по x.

Epsilon YY Model - Веса для регуляризации решения по y.

В группе Parameters:

v0 - Начальное значение приповерхностной скорости.

grad0 - Начальный градиент скорости.

               v(z) = v0 + grad0 * (z - zknots(0))

ds - (Delta zknots)/20 i- длина шага интегрирования по Z,

epsilonxx - вес для регуляризации (минимизация 2-й производной по x от v),

epsilonyy - вес для регуляризации (минимизация 2-й производной по y от v),

epsilonzz - вес для регуляризации (минимизация 2-й производной по z от v),

epsilon - 0.0001*(epsilonxx+epsilonzz) вес для регуляризации (минимизация v),

niteration - максимальное количество итераций.

maxcond – максимально допустимое решение в LSQR 

sigT - допустимая погрешность измерения времени (в 10^-3 сек)

sigM - допустимая погрешность измерения M (iв 10^-9s/(m*m))

maxh - максимальное половинное смещение, которое будет использоваться для усреднения производных скорости (в м)

sigp - допустимая ошибка для горизонтальной медленности (в 10^-6 сек/иетр)

sigxi - допустимая ошибка для положения поверхности (в м)

sigv - допустимая ошибка для априорной скорости (в м / с)

sigvq - допустимый (обратный) вес для минимизации первой производной скорости в касательном направлении локального отражателя

                             0: без минимизации первых производных

sigPxix -допустимая ошибка для горизонтальной медленности в x (в 10 ^ -6 с / м))

sigPxiy - допустимая ошибка для горизонтальной медленности по y (в 10 ^ -6 с / м)

sigXix - допустимая ошибка для положения поверхности x (в м)

sigXiy - допустимая ошибка для положения поверхности y (в м)

Все эти параметры могут быть заданы и сохранены в файле задании с расширением JOB.

Задание запускается кнопкой Start. На экране появляется диалоговое окно Tomography Progress, в котором отображается прохождение задания. Кнопкой Interrupt можно прервать задание в любой момент.

-------------------------------------------------------------------------------------------------------------------------------

Приведем несколько примеров успешного практического применения программы томографии NIP TOMO.

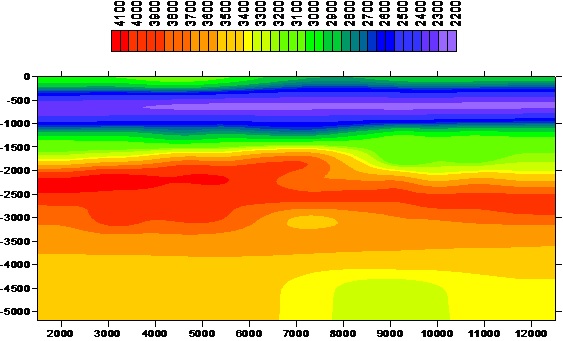
Рис. 1. Пеляткинское ГКМ. Разрез интервальных (пластовых) скоростей по ПР 01. Глубинный масштаб. Получен в результате томографических расчетов программой NIP_TOMO 2-D.

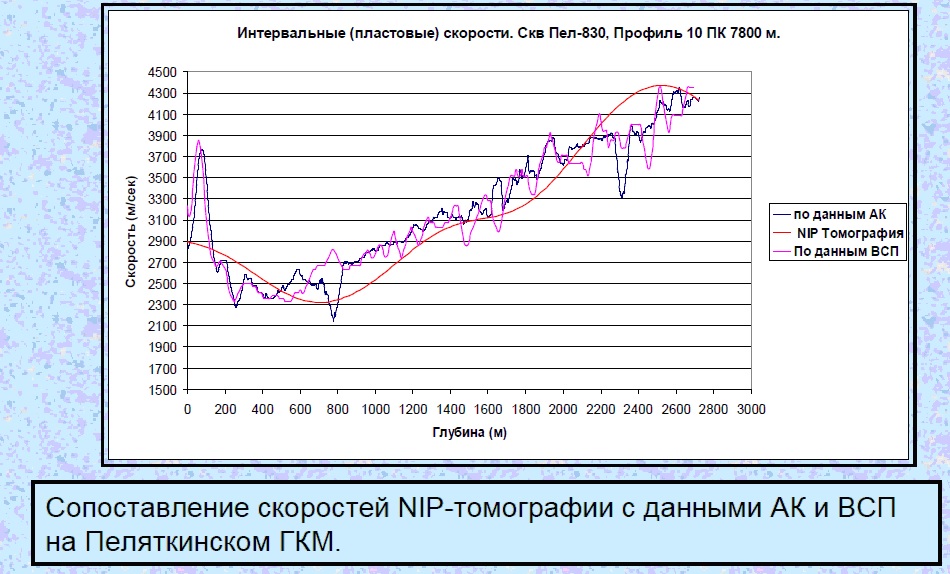
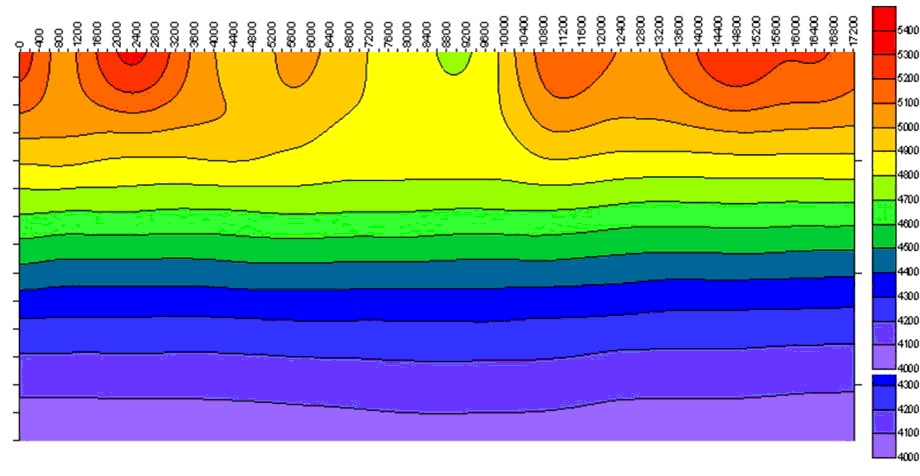
Рис.2. Непско-Ботуобинская антеклиза. Разрез интервальных скоростей по профилю 04, полученный NIP-томографией 2-D.

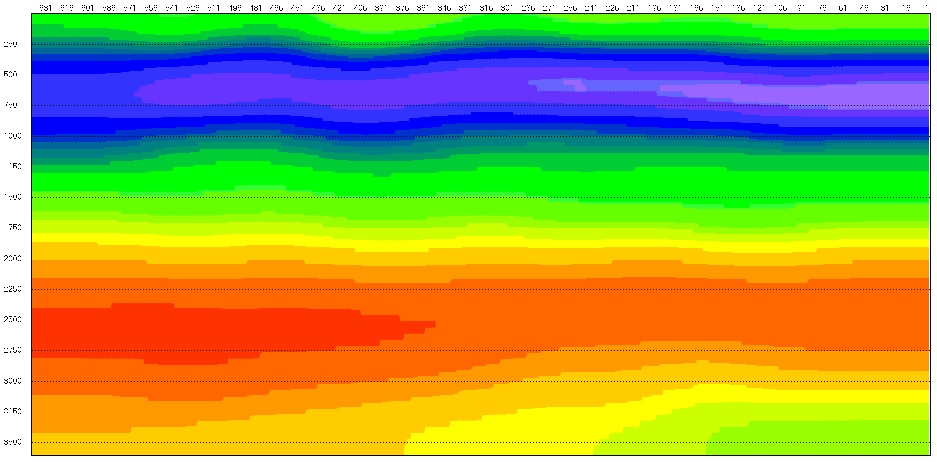
Рис.3. Результат томографической инверсии NIPTOMO 3-D. CrossLine 312. Этот куб получен с заданием Pel_3D.JOB в папке DATAZ\DEMO_3D.

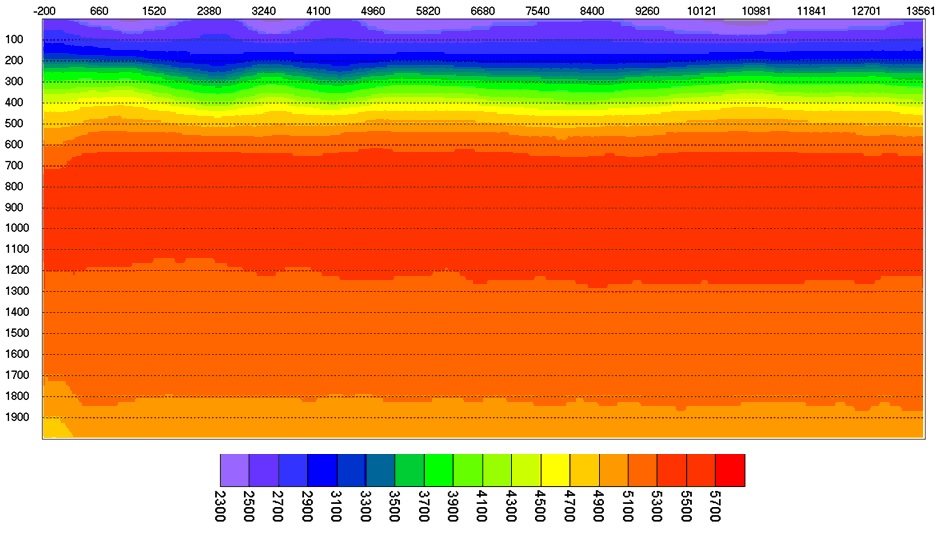
Рис.4. Результат томографической инверсии NIPTOMO 2-D. Якутия. НБА. Мин.V=2300 Макс.V=5800 м/сек. Этот разрез получен с заданием Kurung.JOB в папке DATAZ\DEMO_2D.

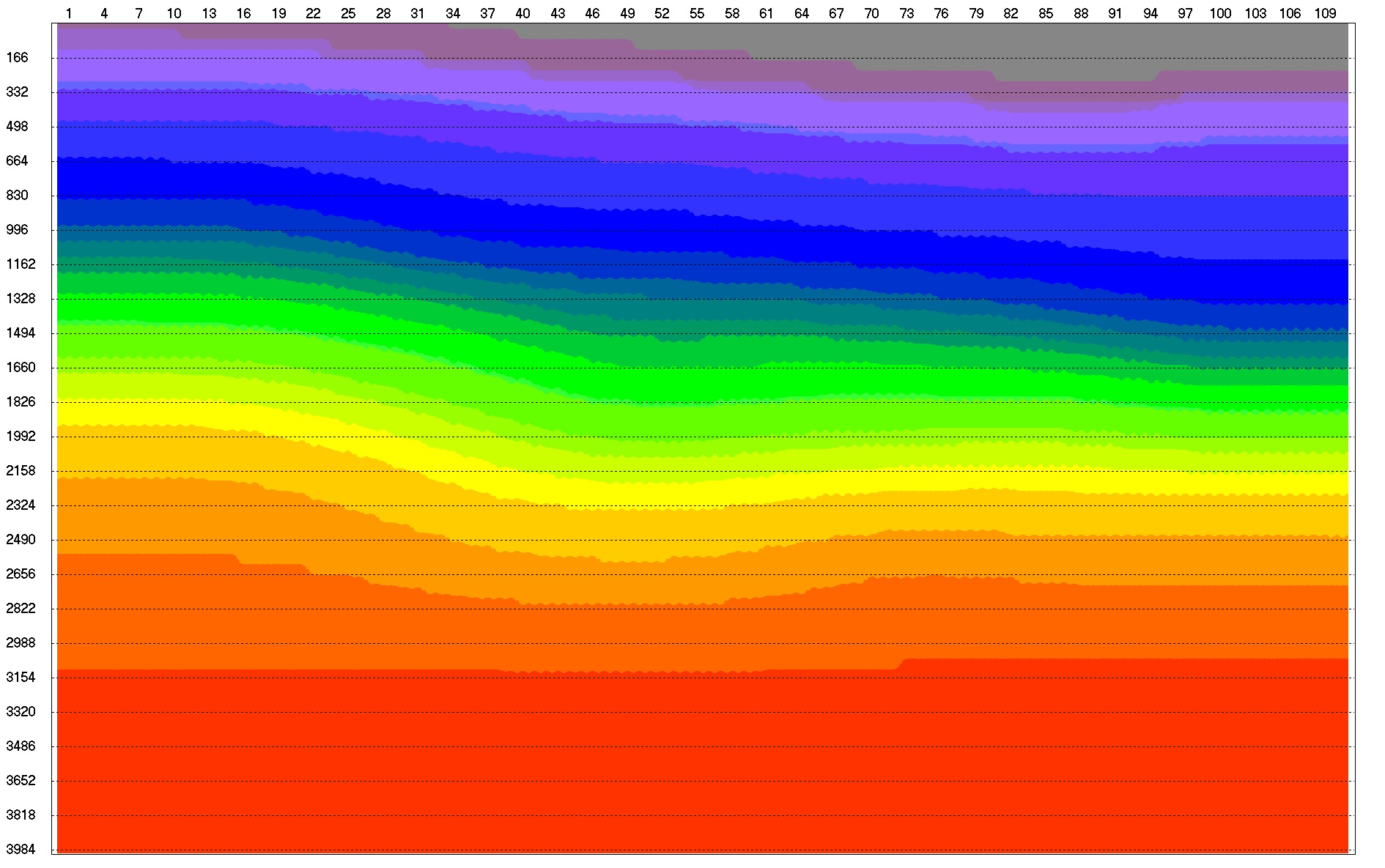
Рис.5. Результат томографической инверсии NIPTOMO 3-D. Тестоые данные. InLine 111. Этот куб получен с заданием Test_tomo_3D.JOB в папке DATAZ\DEMO_3D.

См. также:

Окно прохождения задания

Приведем также инструкцию-комментарий в оригинальной программе Эрика Дувеника.

NIPTOMO - tomographic velocity model estimation on a

          B-splined model using CRS-Stack attributes

USAGE:                                                                

         niptomo dimension= input= output= zknots=                    

REQUIRED PARAMETERS:                                                  

         dimension= -int-     Dimension of the problem:               

                              1  for 1-D inversion                    

                              2  for 2-D inversion                    

                              3  for 3-D inversion                    

                              -1 for 1-D modelling                                        

                              -2 for 2-D modelling                                        

                              -3 for 3-D modelling                                        

-----------------------------------------------------------------------------

REQUIRED PARAMETERS FOR 1-D MODELLING:                                

         input=      -char[]- Input data file name                    

                              [z]=m, z positive downward             

         zknots=     -char[]- Knot sequence (for model description in  

                              z-direction, in m, positive downward) file name 

OPTIONAL PARAMETERS FOR 1-D MODELLING:                                

         output=     -char[]- =\"output.dat\" Output data filename  

                              (final parameters)                    

                              [T]=10^-3s, [M]=10^-9s/m^2, [z]=m     

         endmodel=   -char[]- =\"endmodel.dat\" Final velocity model file name

                               (densely sampled array, ASCII) [v]=m/s   

         startmodel= -char[]- Initial velocity model file name      

                              (B-spline coefficient values in m/s)  

         v0=         -float-  =1500     starting velocity,      [v0]=m/s   

         grad0=      -float-  =0        starting vel. gradient, [grad0]=1/s

                              v(z) = v0 + grad0 * (z - zknots(0))          

                              (only correct if knots are equally spaced in z) \n"

         ds=         -float-  =(Delta zknots)/20 integration step length, [ds]=m \n"    

-----------------------------------------------------------------------------

REQUIRED PARAMETERS FOR 1-D INVERSION:                                              

         input=      -char[]- Input data file name                    

                              [t]=10^-3s, [M]=10^-9s/m^2             

         zknots=     -char[]- Knot sequence (for model description in  

                              z-direction, in m, positive downward) file name 

OPTIONAL PARAMETERS FOR 1-D INVERSION:                                               

         output=     -char[]- =\"output.dat\" Output data filename  

                              (final parameters)                    

                              [T]=10^-3s, [M]=10^-9s/m^2, [z]=m     

         endmodel=   -char[]- =\"endmodel.dat\" Final velocity model file name

                               (densely sampled array, ASCII) [v]=m/s   

         startmodel= -char[]- Initial velocity model file name      

                              (B-spline coefficient values in m/s)  

         v0=         -float-  =1500     starting velocity,      [v0]=m/s   

         grad0=      -float-  =0        starting vel. gradient, [grad0]=1/s

                              v(z) = v0 + grad0 * (z - zknots(0))          

                              (only correct if knots are equally spaced in z) \n"

         ds=         -float-  =(Delta zknots)/20 integration step length, [ds]=m \n"    

         epsilonzz=  -float-  =0.001    weight for regularization   

                              (minimization of 2nd z-derivative of v)          

         epsilon=    -float-  =0.0001*(epsilonxx+epsilonzz)  weight for        

                              regularization (minimization of of v)            

         niteration= -int-    =15       maximum number of iterations            

         maxcond=    -float-  =100000.0  maximum condition number for SVD truncation \n"

         sigT=       -float-  =1    assumed error for time measurement (in 10^-3 s)    

         sigM=       -float-  =1    assumed error for measurements of M (in 10^-9s/(m*m)) \n"

-----------------------------------------------------------------------------

REQUIRED PARAMETERS FOR 2-D MODELLING:                                

         input=      -char[]- Input data file name                    

                              [x]=m, [z]=m, [theta]=degrees, z positive downward

         xknots=     -char[]- Knot sequence (for model description in 

                              x-direction, in m) file name       

         zknots=     -char[]- Knot sequence (for model description in  

                              z-direction, in m, positive downward) file name 

OPTIONAL PARAMETERS FOR 2-D MODELLING:                                

         output=     -char[]- =\"output.dat\" Output data filename  

                              (final parameters)                    

                              [T]=10^-3s, [M_h]=10^-9s/m^2, [p_xi]=10^-6 s/m,

                              [xi]=m, [x]=m, [z]=m, [theta]=degrees    

         endmodel=   -char[]- =\"endmodel.su\" Final velocity model file name

                               (densely sampled array, seismic un*x) [v]=m/s   

         startmodel= -char[]- Initial velocity model file name      

                              (B-spline coefficient values in m/s)  

         v0=         -float-  =1500     starting velocity,      [v0]=m/s   

         grad0=      -float-  =0        starting vel. gradient, [grad0]=1/s

                              v(z) = v0 + grad0 * (z - zknots(0))          

                              (only correct if knots are equally spaced in z) \n"

         ds=         -float-  =(Delta zknots)/20 integration step length, [ds]=m \n"    

         hmax=       -float-  =0.0      maximum  half offset to be used for \n"

                              averaging velocity derivatives (in m)      

-----------------------------------------------------------------------------

REQUIRED PARAMETERS FOR 2-D INVERSION:                                              

         input=      -char[]- Input data file name                    

                              [T]=10^-3s, [M_h]=10^-9s/m^2, [p_xi]=10^-6 s/m, [xi]=m

         xknots=     -char[]- Knot sequence (for model description in 

                              x-direction, in m) file name       

         zknots=     -char[]- Knot sequence (for model description in  

                              z-direction, in m, positive downward) file name 

OPTIONAL PARAMETERS FOR 2-D INVERSION:                                               

         output=     -char[]- =\"output.dat\" Output data filename  

                              (final parameters)                    

                              [T]=10^-3s, [M_h]=10^-9s/m^2, [p_xi]=10^-6 s/m, [xi]=m, \n"

                              [x]=m, [z]=m, [theta]=degrees    

         vinput=     -char[]- File containing a priori velocity information: \n"

                              x  z  v(x,z), where [x]=[z]=m, [v]=m/s \n"

         voutput=    -char[]- =\"voutput.dat\"  Name of output file, containing \n"

                              the a priori velocity information together with the \n"

                              corresponding obtained values:  x  z  v(x,z)  v_out(x,z), \n"

                              where [x]=[z]=m, [v]=[v_out]=m/s \n"

         endmodel=   -char[]- =\"endmodel.su\" Final velocity model file name

                               (densely sampled array, seismic un*x) [v]=m/s   

         startmodel= -char[]- Initial velocity model file name      

                              (B-spline coefficient values in m/s)  

         v0=         -float-  =1500     starting velocity,      [v0]=m/s   

         grad0=      -float-  =0        starting vel. gradient, [grad0]=1/s

                              v(z) = v0 + grad0 * (z - zknots(0))          

                              (only correct if knots are equally spaced in z) \n"

         ds=         -float-  =(Delta zknots)/20 integration step length, [ds]=m \n"    

         hmax=       -float-  =0.0      maximum  half offset to be used for \n"

                              averaging velocity derivatives (in m)      

         epsilonzz=  -float-  =0.001    weight for regularization   

                              (minimization of 2nd z-derivative of v)          

         epsilonxx=  -float-  =epsilonzz   weight for regularization   

                              (minimization of 2nd x-derivative of v)

         epsilon=    -float-  =0.0001*(epsilonxx+epsilonzz)  weight for        

                              regularization (minimization of of v)            

         epsilonxxmodel= -char[]- Spatially varying weights for epsilonxx regularization \n"

                              (B-spline coefficient values (1 - 100), default: 1) \n"

         epsilonzzmodel= -char[]- Spatially varying weights for epsilonzz regularization \n"

                              (B-spline coefficient values (1 - 100), default: 1) \n"

         niteration= -int-    =15       maximum number of iterations            

         maxcond=    -float-  =10000.0  maximum condition number in LSQR        

         sigT=       -float-  =1    assumed error for time measurement (in 10^-3 s)    

         sigM=       -float-  =1    assumed error for measurements of M (in 10^-9s/(m*m)) \n"

         sigp=       -float-  =2    assumed error for horizontal slowness (in 10^-6 s/m)

         sigxi=      -float-  =1    assumed error for surface position (in m)      

         sigv=       -float-  =1    assumed error for a priori velocity (in m/s)    

         sigvq=      -float-  =0    assumed  (inverse) weight for minimization of first

                              derivative of velocity in local reflector tangent direction \n"

                              0: no minimization of first derivatives                  

-----------------------------------------------------------------------------

REQUIRED PARAMETERS FOR 3-D MODELLING:                                

         input=      -char[]- Input data file name                    

                              [azimuth]=degrees, [x]=m, [y]=m, [z]=m, 

                              [ex]=10^-3,[ey]=10^-3; z positive downward \n"

        xknots=     -char[]- Knot sequence (for model description in 

                              x-direction, in m) file name            

         yknots=     -char[]- Knot sequence (for model description in 

                              y-direction, in m) file name            

         zknots=     -char[]- Knot sequence (for model description in 

                              z-direction, in m, positive downward) file name \n"

OPTIONAL PARAMETERS FOR 3-D MODELLING:                                

         output=     -char[]- =\"output.dat\" Output data filename    

                              (final parameters)                      

                              [T]=10^-3s, [M_azimuth]=10^-9s/m^2 [Pxix]=10^-6s/m,

                              [Pxiy]=10^-6s/m, [Xix]=m, [Xiy]=m, [azimuth]=degrees, \n"

[x]=m, [y]=m, [z]=m, [ex]=10^-3,[ey]=10^-3;  

(M_azimuth = d^2T/dh_azimuth^2  !!!)         

         endmodel=   -char[]- =\"endmodel.su\" Final velocity model file name \n"

                               (densely sampled array, seismic un*x) [v]=m/s

         startmodel= -char[]- Initial velocity model file name             

                              (B-spline coefficient values in m/s)         

         v0=         -float-  =1500     starting velocity,      [v0]=m/s   

         grad0=      -float-  =0        starting vel. gradient, [grad0]=1/s

                              v(z) = v0 + grad0 * (z - zknots(0))          

                              (only correct if knots are equally spaced in z) \n"

         ds=         -float-  =(Delta zknots)/20 integration step length, [ds]=m \n"    

         hmax=       -float-  =0.0      maximum  half offset to be used for

                              averaging velocity derivatives (in m)        

----------------------------------------------------------------------------

REQUIRED PARAMETERS FOR 3-D INVERSION:                                 

         input=      -char[]- Input data file name                    

                              [T]=10^-3s, [M_azimuth]=10^-9s/m^2 [Pxix]=10^-6s/m,

                              [Pxiy]=10^-6s/m, [Xix]=m, [Xiy]=m, [azimuth]=degrees \n"

         xknots=     -char[]- Knot sequence (for model description in 

                              x-direction, in m) file name            

         yknots=     -char[]- Knot sequence (for model description in 

                              y-direction, in m) file name            

         zknots=     -char[]- Knot sequence (for model description in 

                              z-direction, in m, positive downward) file name \n"

OPTIONAL PARAMETERS FOR 3-D INVERSION:                                 

         output=     -char[]- =\"output.dat\" Output data filename  

                              (final parameters)                    

                              [T]=10^-3s, [M_azimuth]=10^-9s/m^2 [Pxix]=10^-6s/m,

                              [Pxiy]=10^-6s/m, [Xix]=m, [Xiy]=m, [azimuth]=degrees, \n"

[x]=m, [y]=m, [z]=m, [ex]=10^-3,[ey]=10^-3;  

(M_azimuth = d^2T/dh_azimuth^2  !!!)         

         vinput=     -char[]- File containing a priori velocity information: \n"

x  y  z  v(x,y,z), where [x]=[y]=[z]=m, [v]=m/s \n"

voutput=    -char[]- =\"voutput.dat\"  Name of output file, containing \n"

                              the a priori velocity information together with the \n"

                              corresponding obtained values:  x  y  z  v(x,y,z)  v_out(x,y,z), \n"

                              where [x]=[y]=[z]=m, [v]=[v_out]=m/s \n"

         endmodel=   -char[]- =\"endmodel.su\" Final velocity model file name

                               (densely sampled array, seismic un*x) [v]=m/s   

         startmodel= -char[]- Initial velocity model file name      

                              (B-spline coefficient values in m/s)  

         v0=         -float-  =1500     starting velocity,      [v0]=m/s   

         grad0=      -float-  =0        starting vel. gradient, [grad0]=1/s

                              v(z) = v0 + grad0 * (z - zknots(0))          

                              (only correct if knots are equally spaced in z) \n"

         ds=         -float-  =(Delta zknots)/20 integration step length, [ds]=m \n"    

         hmax=       -float-  =0.0      maximum  half offset to be used for \n"

                              averaging velocity derivatives (in m)      

         epsilonzz=  -float-  =0.001    weight for regularization   

                              (minimization of 2nd z-derivative of v)          

         epsilonxx=  -float-  =epsilonzz   weight for regularization   

                              (minimization of 2nd x-derivative of v)

         epsilonyy=  -float-  =epsilonzz   weight for regularization   

                              (minimization of 2nd y-derivative of v)

         epsilon=    -float-  =0.0001*(epsilonxx+epsilonzz)  weight for        

                              regularization (minimization of of v)            

         epsilonxxmodel= -char[]- Spatially varying weights for epsilonxx regularization \n"

                              (B-spline coefficient values (1 - 100), default: 1) 1-D array

         epsilonyymodel= -char[]- Spatially varying weights for epsilonyy regularization \n"

                              (B-spline coefficient values (1 - 100), default: 1) 1-D array

         niteration= -int-    =15       maximum number of iterations            

         maxcond=    -float-  =10000.0  maximum condition number in LSQR        

         sigT=       -float-  =1    assumed error for time measurement (in 10^-3 s)        

         sigM=       -float-  =1    assumed error for measurements of M (in 10^-9s/(m*m)) \n"

         sigPxix=    -float-  =2    assumed error for horizontal slowness in x (in 10^-6 s/m)

         sigPxiy=    -float-  =2    assumed error for horizontal slowness in y (in 10^-6 s/m)

         sigXix=     -float-  =1    assumed error for surface position x (in m)      

         sigXiy=     -float-  =1    assumed error for surface position y (in m)      

         sigv=       -float-  =1    assumed error for a priori velocity (in m/s)

         sigvq=      -float-  =0    assumed  (inverse) weight for minimization of first

                              derivative of velocity in local reflector tangent direction \n"

                              0: no minimization of first derivatives                  

----------------------------------------------------------------------------------

         All one-dimensional arrays have to be given as row vectors.           

         The final velocity model B-spline coefficient values (in m/s)          

         are written into \"_endmodel.dat_\".                                  

AUTHOR:                                                                        

         Eric Duveneck                                                         

         eric.duveneck@gpi.uni-karlsruhe.de

К началу раздела.

К началу инструкции