Процедура FILRG
Рекурсивная остронаправленная режекторная фильтрация.
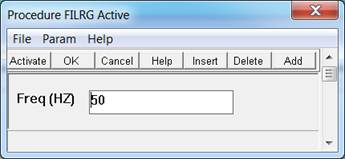
Параметр:
FREQ - частота режекции в герцах (целое или действительное число).
Частота задается именно в герцах (независимо от значения делителя времен).
Программу следует применять по исходным сейсмограммам до каких-либо регулировок амплитуд.
Линейную фильтрацию можно осуществить несколькими способами: сверткой импульсных реакций, умножением спектров и, наконец – умножением полиномов Z-преобразований. Последний метод дает возможность синтезировать чрезвычайно эффективные рекурсивные фильтры с бесконечной длиной оператора.
Попытаемся синтезировать
такой фильтр 
, Z-преобразование которого представлено соотношением
полиномов
(1)
Сразу отметим, что такой фильтр будет каузальным (причинным), поскольку не содержит отрицательных степеней Z.
В результате деления полиномов чаще всего получаем полином бесконечной размерности
(2)
Поэтому, реализовать такой фильтр сверткой или произведением спектров невозможно.
С учетом (1) процесс фильтрации входного сигнала X(Z) принимает вид:
(3)
Умножив левую
и правую части этого уравнения на 
, получаем
(4)
Последнее выражение имитирует
действие аналогового усилителя с обратной связью. Появление множителя Z перед 
вызывает
задержку 
на единицу времени 
.
Выходной сигнал формируется как разность действий фильтра 
на 
и
фильтра 
на задержанную во времени .
Из выражения (4) легко
получить выражение для n-го отсчета
временного ряда 
(5)
Значение 
определяется
через предыдущие значения 
и 
. Уравнение (5)
описывает алгоритм рекурсивной фильтрации. Отметим, что рекурсивный фильтр
будет устойчивым лишь при условии, что фильтр в
знаменателе 
будет минимально-фазовым.
Проиллюстрируем
схему синтеза рекурсивного фильтра построением простого острорежекторного
фильтра, подавляющего лишь одну заданную гармонику 
.
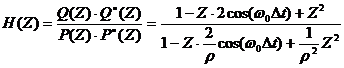(6)
Согласно (5) получаем окончательное выражение для цифровой рекурсивной фильтрации.
(7)
Как видим, качественная режекторная фильтрация может быть осуществлена
пятиточечным рекурсивным оператором, что не идет ни в какое сравнение с длиною
простого сверточного фильтра. Однако, не следует забывать, что рекурсивному фильтру присущи
такие черты как неустойчивость при малых значениях 
и
чувствительность к нестационарности гармоники 
.
Краевые искажение сильнее проявляются при рекурсивной фильтрации (рис. 2.33),
поскольку пятиточечная рекурсия аппроксимирует сверточный
фильтр бесконечной длины.
Фильтр (7) не является нуль-фазовым. С целью избежания фазовых искажений, рекурсия осуществляется поочередно в двух направлениях.