Методические рекомендации по применению
преобразования Радона.
Преобразование
Радона (более известное в сейсморазведке как tau-p
преобразование) - интегральное преобразование функции многих переменных,
родственное преобразованию Фурье. Впервые введено в работе австрийского
математика Иоганна Радона 1917-го года. Важнейшее свойство преобразования
Радона — обратимость, то есть возможность восстанавливать исходную функцию по
её преобразованию Радона.
Прямое преобразования
Радона определяется как:
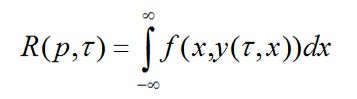
где x - расстояние от источника к приемнику, p - направляющий вектор tau - пересечение кривой y с
осью y в точке x=0.
Очевидно, что в прямом преобразовании Радона интегрирование осуществляется
вдоль аналитической кривой y.
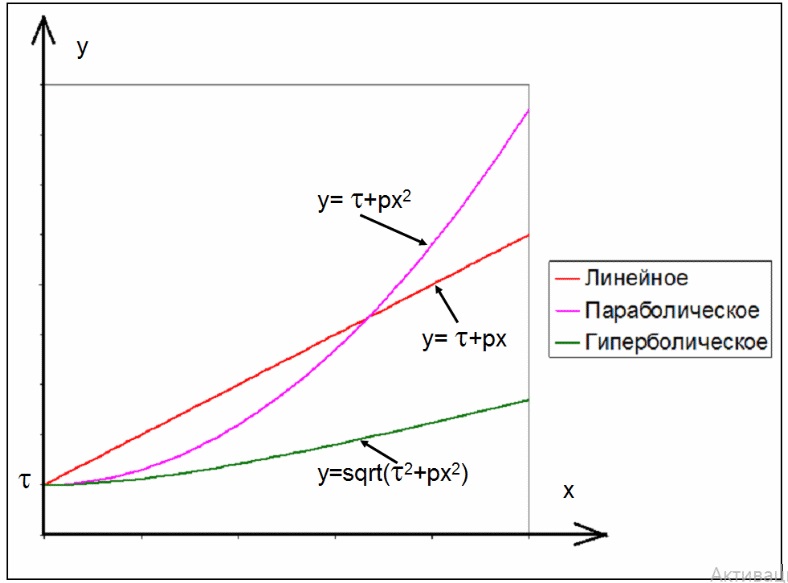
Траектории
интегрирования в прямом преобразовании Радона.
Линия в исходных
данных f в процессе прямого преобразования Радона изображается
в виде точки (tau,p).
Преобразования могут осуществляться для различных траекторий (направляющие
векторы), по которым выполняется анализ трасс с целью определения сходства. В
каждом отдельном случае значение параметра p будут различными.
Обратное
преобразование Радона осуществляется в два этапа. На первом этапе выполняется
свертка каждой трассы R
с оператором
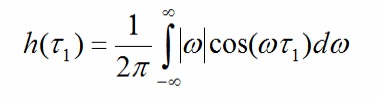
результатом которой являются модифицированные
проекции R’ .
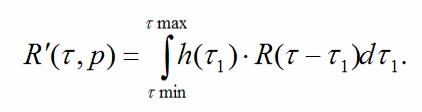
На втором этапе осуществляется обратное
проецирование.
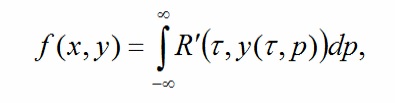
где y - обращенный во времени направляющий вектор.
Например, для линейного преобразования y=tau-px .
Представленный Алгоритм называется
сверточным. Существуют и другие методы реконструкции f из R .
Ниже представлены
прямые преобразования Радона по различным траекториям набора синтетических
"прямых волн".
Прямое
преобразования Радона. А - исходная сейсмограмма, Б - линейные направляющие
векторы, В - параболические направляющие векторы, Г - гиперболические
направляющие векторы.
Ниже представлены
обратные преобразования Радона по различным траекториям набора синтетических
"прямых волн".

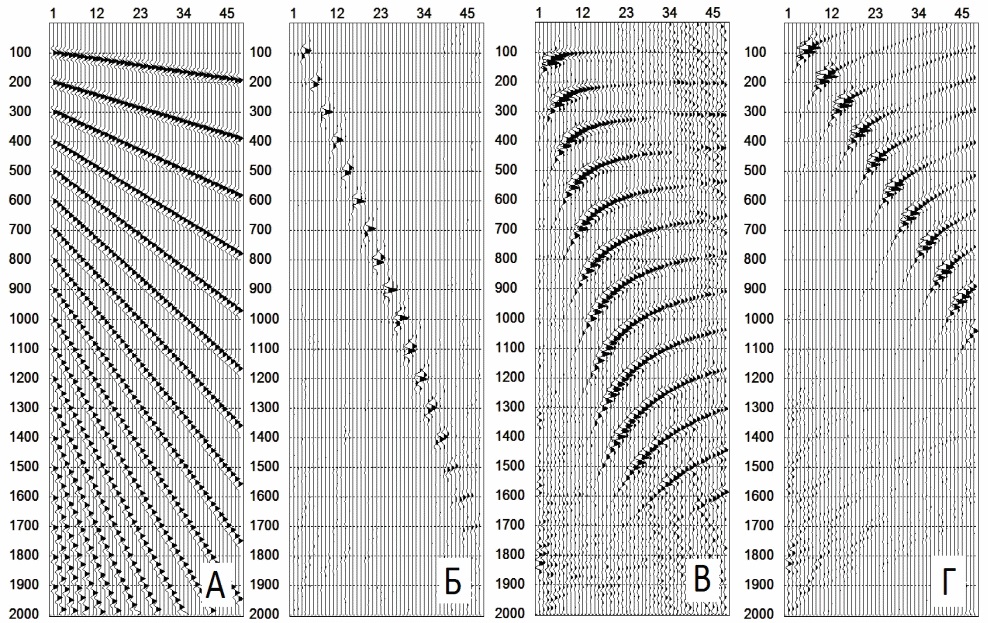
Обратное
преобразования Радона. А - исходная сейсмограмма, Б - линейные направляющие
векторы, В - параболические направляющие векторы, Г - гиперболические
направляющие векторы.
Ниже представлены прямые
преобразования Радона по различным траекториям набора синтетических
"отраженных волн".
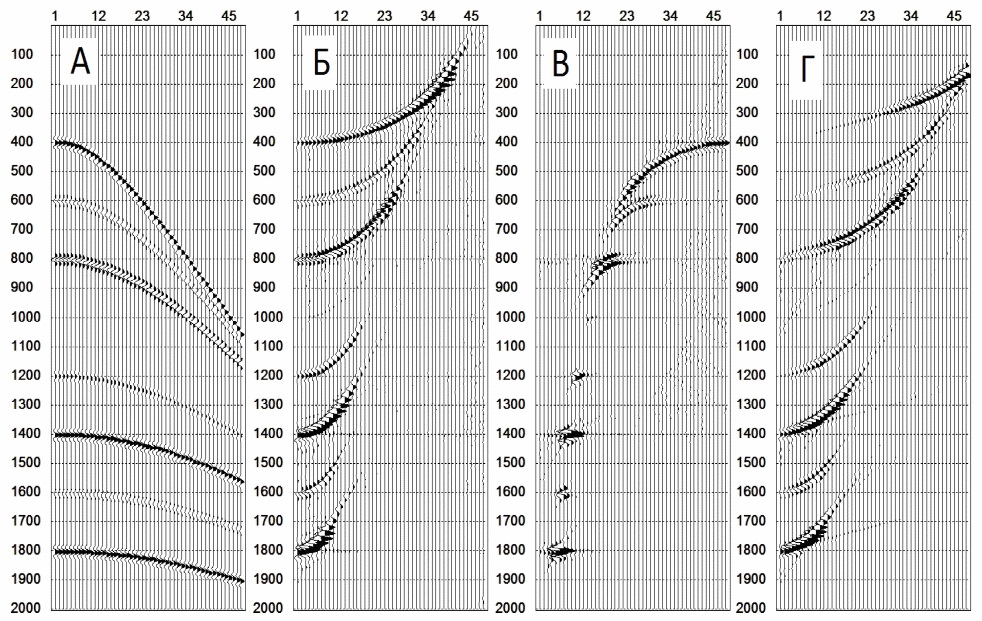
Прямое
преобразования Радона. А - исходная сейсмограмма, Б - линейные направляющие
векторы, В - параболические направляющие векторы, Г - гиперболические
направляющие векторы.
Ниже представлены
обратные преобразования Радона по различным траекториям набора синтетических
"отраженных волн".
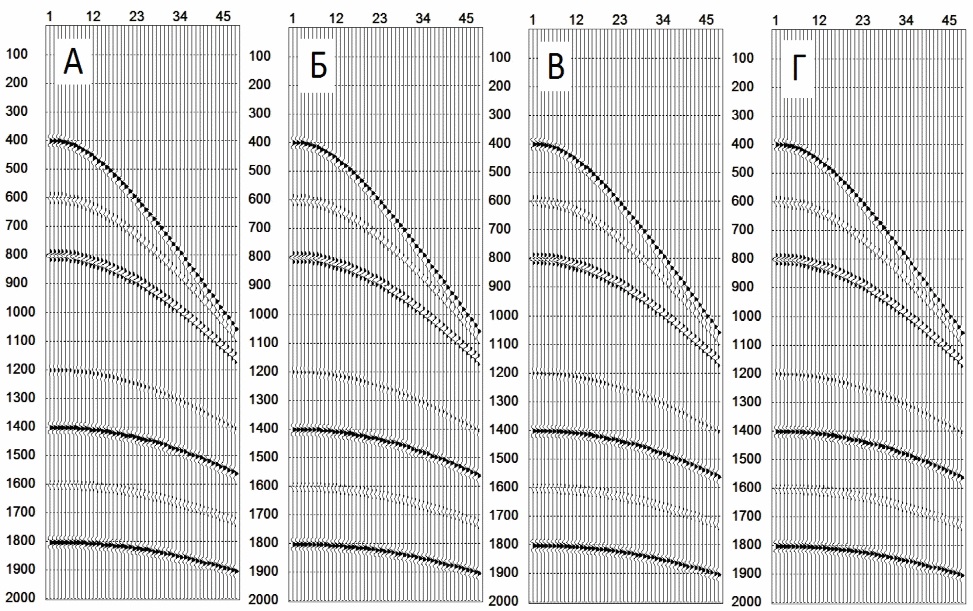
Обратное
преобразования Радона. А - исходная сейсмограмма, Б - линейные направляющие
векторы, В - параболические направляющие векторы, Г - гиперболические
направляющие векторы.
В современных
пакетах обработки данных сейсморазведки создано несколько методик применения
преобразования Радона. В качестве примеров можно привести интерполяцию между
трассами, фильтрацию наклонов, подавление кратных волн, обращение преломленной
волны, миграцию и скоростной анализ.
Наиболее
распространенным является применение параболического пребразования Радона с
целью подавления кратных отраженных волн.
Преобразование гиперболических осей синфазности в параболы перед прямым
преобразованием Радона осуществляется одним из двух способов:
1. Ввод кинематических поправок в
соответствии со соростями суммирования Vnmo процедурой NMO.
2. "Растяжение" трассы
преобразованием оси времен T0 в ось квадратов времен T02
процедурой T2_STR.
Оба метода имеют как достоинства, так и
недостатки. Первый метод обеспечивает относительно небольшой диапазон задания
кинематических поправок и малый шаг расчета трасс в преобразовании Радона.
Однако он приводит к сильному растяжению сигнала на малых временах, а
остаточная парабола является приближенной. Второй метод не искажает сигнал и
превращает гиперболу в точную параболу. Однако требует большего диапазона
кинематических поправок в преобразовании Радона.